日志

奥数比赛，难题求解（三） --- 证明中间条件

热度 1已有 704 次阅读2015-7-26 12:29 |个人分类:逻辑分析|系统分类:原创博文 | 宽屏请点击显示宽屏，再点击恢复窄屏 | 动漫全图如只见部分动漫，请点击显示全图，再点击恢复窄图

原题可见：《奥数比赛，难题求解（一） --- 题目》
题解可见：《奥数比赛，难题求解（二） --- 题解》

由上面题解中，题目已经得到证明，在两个假定之上：P在BC的延长线上，且：PH⊥HQ，我们来验证这两个假定。

证明：

1）。P在BC的延长线上，

过D,H，K三点的圆，其圆心P在在BC的延长线上，这是显而易见的事实：HF=DF，即：三角形的垂心到一边的距离，等于这边上的高线的延长线从垂足到外接圆的长度。我们可以认为这是一条定理，也很容易证明。下图中：

连接DC，延长CH交AB于E,则，AE是AB的高线：AB⊥AE。此时，ΔCHF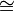 $\cong$ ΔCDF，这是因为，两个都是直角三角形，有一个共同的边，且：∠CHF=∠CDF （∠CHF=90°-∠ECB=∠ABC=∠ADC（圆周角定理）=∠CDF）

于是：HF=DF，ΔPHF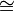 $\cong$ ΔPDF，P与BC共线，证毕。

2）。PH⊥HQ，

过H点做：直线RHT⊥PH，相交于圆r于R，T，则RHT切圆KHD于切点H。于是：∠RHK=∠HDK（弦切角定理）=∠ADK=∠AQ’K，于是： AQ’∥RT

显而易见：AQ’∥QA’（因为AA'和QQ’分别是圆的直径），所以：QA’∥RT。又因为：QHMA’四点共线；所以过H点的两条平行直线：QHMA’和RHT共线，即有：PH⊥HQ，证毕。

注意：上面证明中，仍旧有两条：1）。QHMA’四点共线；2）。KHQ’三点共线；待证，见本文：（四）。